تطوير شبكة عصبية في Python بدون استخدام TensorFlow أو PyTorch

في هذا الدليل، سنبدأ بشرح المفاهيم الأساسية التي تقف خلف الشبكات العصبية، وسنقوم بتوضيح كيفية بناء هذه المفاهيم في Python باستخدام مكتبة numpy. بعد فهم هذه المفاهيم، سنتناول مشكلة XOR الشهيرة وسنقوم بحلها باستخدام شبكة عصبية بسيطة.

المفاهيم الأساسية

قبل بناء شبكة عصبية، من المهم فهم بعض المفاهيم الأساسية. هذه المفاهيم تشمل:

• دوال التفعيل (Activation Functions): تحول المدخلات عبر كل طبقة إلى شكل غير خطي.
• التفعيل الأمامي (Forward Propagation): حساب الإخراج النهائي عبر تمرير البيانات من طبقة الإدخال إلى الإخراج.
• الانتشار العكسي (Backpropagation): تحديث الأوزان باستخدام التدرجات بناءً على الخطأ الذي يتم حسابه في كل طبقة.
• تهيئة الأوزان (Weight Initialization): اختيار قيم مناسبة للأوزان للبدء بشكل صحيح في عملية التدريب.

1. دوال التفعيل (Activation Functions)

دوال التفعيل هي جزء أساسي من الشبكات العصبية لأنها تحول البيانات في كل طبقة إلى شكل غير خطي. بدونها، ستكون الشبكة مجرد شبكة خطية، مما يحد من قدرتها على التعلم.

أشهر دوال التفعيل هي Sigmoid وTanh. سنستخدمهما في شبكة XOR:

import numpy as np

# دالة تفعيل Sigmoid
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# دالة تفعيل Tanh
def tanh(x):
    return np.tanh(x)

# مشتقات دوال التفعيل لاستخدامها في الانتشار العكسي
def sigmoid_derivative(x):
    return x * (1 - x)

def tanh_derivative(x):
    return 1 - np.tanh(x) ** 2

تعمل دالة Sigmoid على تحويل المدخلات إلى نطاق بين 0 و 1، مما يجعلها مفيدة في مهام التصنيف. أما Tanh فتعمل على تحويل المدخلات إلى نطاق بين -1 و 1، وهي مناسبة للطبقات المخفية لأنها تتعامل بشكل أفضل مع البيانات غير الخطية.

2. التفعيل الأمامي (Forward Propagation)

في التفعيل الأمامي، تمر البيانات من خلال الشبكة العصبية عبر الطبقات المختلفة حتى تصل إلى طبقة الإخراج. في هذه العملية، نقوم بحساب ناتج كل طبقة بناءً على الأوزان ودالة التفعيل.

# التفعيل الأمامي
def forward(X, W1, W2):
    z1 = np.dot(X, W1)
    a1 = tanh(z1)
    z2 = np.dot(a1, W2)
    a2 = sigmoid(z2)
    return a2, a1

هنا يتم تمرير البيانات من طبقة الإدخال إلى الطبقة المخفية باستخدام tanh، ثم إلى طبقة الإخراج باستخدام sigmoid. في كل طبقة نقوم بحساب ناتج الدالة بناءً على المدخلات والأوزان.

3. الانتشار العكسي (Backpropagation)

الانتشار العكسي هو العملية التي يتم فيها تحديث الأوزان بناءً على الخطأ الذي يتم حسابه بين النتيجة المتوقعة والنتيجة الفعلية. في هذه العملية، نستخدم مشتقات دوال التفعيل لحساب التدرجات وتحديث الأوزان.

# الانتشار العكسي
def backward(X, y, W1, W2, a1, a2, learning_rate):
    error_output = y - a2
    delta_output = error_output * sigmoid_derivative(a2)

    error_hidden = delta_output.dot(W2.T)
    delta_hidden = error_hidden * tanh_derivative(a1)

    # تحديث الأوزان
    W2 += a1.T.dot(delta_output) * learning_rate
    W1 += X.T.dot(delta_hidden) * learning_rate

    return W1, W2

في هذه العملية، يتم حساب الفرق بين التوقعات والإجابات الحقيقية، ثم يتم تحديث الأوزان باستخدام التدرجات التي تم حسابها.

4. تهيئة الأوزان (Weight Initialization)

يتم تهيئة الأوزان بشكل عشوائي عند بدء تدريب الشبكة العصبية. نستخدم تقنية Xavier Initialization لضبط الأوزان بشكل مناسب.

# Xavier initialization for better weight scaling
def xavier_initialization(input_size, output_size):
    return np.random.randn(input_size, output_size) * np.sqrt(1 / input_size)

مشكلة XOR: الشرح والحل

الآن وبعد أن فهمنا المفاهيم الأساسية، دعونا ننتقل إلى مشكلة XOR. هذه المشكلة تتطلب من الشبكة العصبية التعرف على الأنماط غير الخطية. النتيجة المتوقعة لمجموعة بيانات XOR هي:

0 XOR 0 = 0
0 XOR 1 = 1
1 XOR 0 = 1
1 XOR 1 = 0

حل مشكلة XOR باستخدام الشبكة العصبية

لحل مشكلة XOR، سنستخدم شبكة عصبية بسيطة تتكون من طبقة إدخال، طبقة مخفية، وطبقة إخراج. سنقوم باستخدام دالة tanh في الطبقة المخفية وsigmoid في الطبقة الأخيرة.

الكود الكامل لبناء وتدريب الشبكة العصبية على XOR

import numpy as np
import matplotlib.pyplot as plt

# Fixing the random seed for reproducibility
np.random.seed(42)

# دوال التفعيل ومشتقاتها
def tanh(x):
    return np.tanh(x)

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def tanh_derivative(x):
    return 1 - np.tanh(x) ** 2

def sigmoid_derivative(x):
    return x * (1 - x)

# Xavier initialization for better weight scaling
def xavier_initialization(input_size, output_size):
    return np.random.randn(input_size, output_size) * np.sqrt(1 / input_size)

# التفعيل الأمامي
def forward(X, W1, W2):
    z1 = np.dot(X, W1)
    a1 = tanh(z1)
    z2 = np.dot(a1, W2)
    a2 = sigmoid(z2)
    return a2, a1

# الانتشار العكسي
def backward(X, y, W1, W2, a1, a2, learning_rate):
    error_output = y - a2
    delta_output = error_output * sigmoid_derivative(a2)

    error_hidden = delta_output.dot(W2.T)
    delta_hidden = error_hidden * tanh_derivative(a1)

    W2 += a1.T.dot(delta_output) * learning_rate
    W1 += X.T.dot(delta_hidden) * learning_rate

    return W1, W2

# إعداد البيانات
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y = np.array([[0], [1], [1], [0]])

# إعداد الأوزان باستخدام Xavier initialization
input_size = 2
hidden_size = 4
output_size = 1
W1 = xavier_initialization(input_size, hidden_size)
W2 = xavier_initialization(hidden_size, output_size)

# التدريب
epochs = 20000
learning_rate = 0.01
losses = []

for epoch in range(epochs):
    a2, a1 = forward(X, W1, W2)
    W1, W2 = backward(X, y, W1, W2, a1, a2, learning_rate)

    loss = np.mean(np.square(y - a2))
    losses.append(loss)
    if epoch % 1000 == 0:
        print(f'Epoch {epoch}, Loss: {loss}')

# تقييم أداء الشبكة
predictions = np.round(a2)
accuracy = np.mean(predictions == y)
print(f'Accuracy: {accuracy * 100}%')

# عرض الخسارة
plt.plot(losses)
plt.title('Loss over time')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.show()

Download from Github

بعد تشغيل الكود، سنرى النتائج التالية في وحدة التحكم (console):

Epoch 0, Loss: 0.26826273600682626
Epoch 1000, Loss: 0.24384160718733663
Epoch 2000, Loss: 0.24013321393176976
Epoch 3000, Loss: 0.2354515952566291
Epoch 4000, Loss: 0.22958891131789833
Epoch 5000, Loss: 0.22161540871163943
Epoch 6000, Loss: 0.20839297164637977
Epoch 7000, Loss: 0.1850165148502373
Epoch 8000, Loss: 0.1530246516356506
Epoch 9000, Loss: 0.12392443061829908
Epoch 10000, Loss: 0.10408311463980328
Epoch 11000, Loss: 0.09186530177027093
Epoch 12000, Loss: 0.08430071432955208
Epoch 13000, Loss: 0.07941460393309893
Epoch 14000, Loss: 0.07610281203175959
Epoch 15000, Loss: 0.07375699799490315
Epoch 16000, Loss: 0.07203144846297771
Epoch 17000, Loss: 0.0707211724402877
Epoch 18000, Loss: 0.06969932290264914
Epoch 19000, Loss: 0.06888426615934315
Accuracy: 100.0%

بعد الانتهاء، سيعرض البرنامج الشكل التالي الذي يوضح نفس النتائج كمنحنى يصف تطور الخسارة خلال الحلقات التدريبية (epochs).

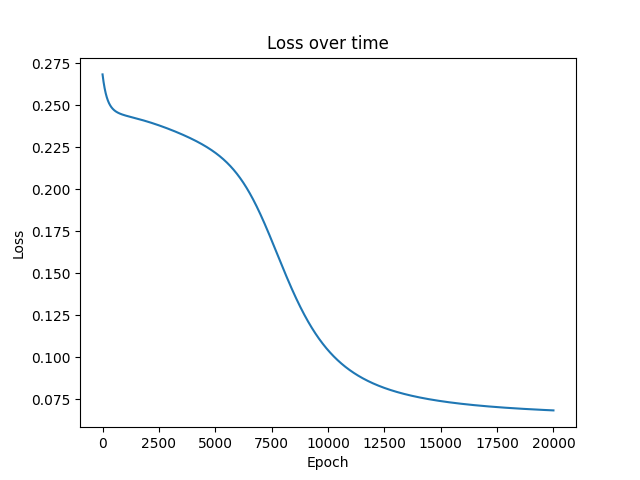
الخلاصة

قمنا في هذا الدليل ببناء شبكة عصبية بسيطة من الصفر باستخدام Python وnumpy لحل مشكلة XOR. شرحنا المفاهيم الأساسية مثل التفعيل الأمامي والانتشار العكسي، ثم قمنا بتطبيقها على مجموعة بيانات XOR. باستخدام هذا الحل، يمكن للشبكة العصبية تعلم الأنماط غير الخطية بنجاح.